Bovine Brain Damage: New Findings in the Field of Wildlife Neuroscience
Gretchen Carpenter ’23, Neuroscience, 22F In May 2022, Ackermans et al. from the Icahn School of Medicine at Mount Sinai published an intriguing study, directly contradicting the previous commonly held understanding that humans were the only animals to suffer from chronic traumatic encephalopathy (CTE). The findings? Headbutting muskoxen showed signs...
The Heredity of Mental Disorders
Elizabeth (Shuxuan) Li ’25, Neuroscience, 22F If you were a prospective parent with a mental disorder, would your children be more at risk for your specific condition or mental illnesses in general? Mental health data from Dr. Jill Goldstein’s research team showed that children at risk for any psychological condition...
Levels of Empathy in Apes and Humans
Elizabeth (Shuxuan) Li ’25, Biological Sciences, 22F One day at the San Diego Zoo, an old male bonobo named Kakowet suddenly began screaming and frantically waving his arms at the zookeepers. After noticing Kakowet’s odd behavior, the keepers checked his surroundings to find several young bonobos stuck in a two-meter-deep...
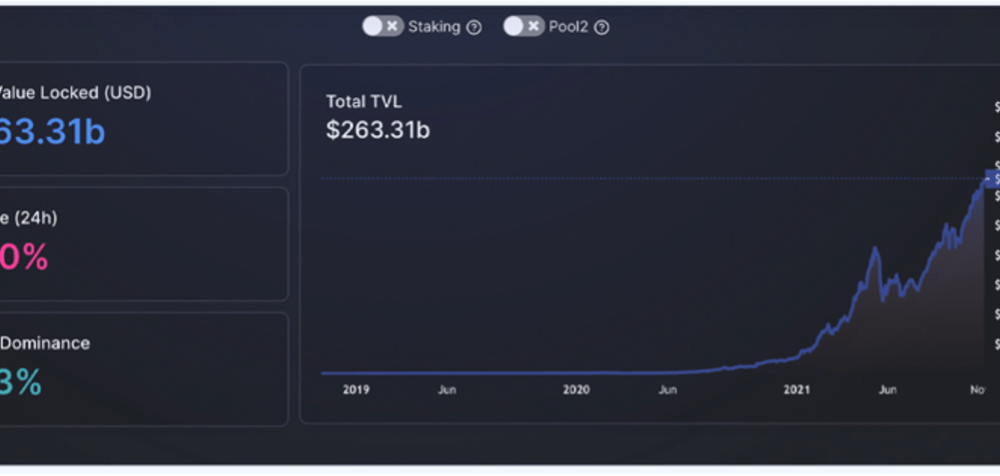
Stochastic Volatility Models and its Effect on the Asset Market
Nandkishor J, Applied Sciences, 22F This paper delves into the significance of Stochastic Volatility (SV), a fundamental economic concept used in determining patterns and fluctuations in asset market prices. Stochastic refers to a random probability distribution or pattern that can be statistically analyzed but cannot be precisely predicted. Attempting to...
Corporate Psychopathy: Does Empathy Cripple Leaders?
Avi Srivastava, Applied Sciences, 22F The Diagnostic and Statistical Manual of Mental Disorders (DSM) has long been able to comprehensively document the consequences of affective interactive traits like egocentricity and consistent manipulation that drive psychopaths within interpersonal relationships. However, in a recent trend, Anti-Social Personality Disorder (ASPD), has garnered an...
Dementia Villages – Experimenting with Universal Design Treatment
Avi Srivastava, Applied Sciences, 22F A case of dementia is diagnosed in the world every 3.2 seconds. With the number of patients expected to almost triple to 140 million by 2050 as we live longer—coupled with contemporary anti-dementia medicines and disease-modifying therapies still showing little promise—the search for new safe...
Social Media, Dopamine, and Stress: Converging Pathways
Valentina Fernandez ’24, Neuroscience, 22X Figure: Social networking has experienced tremendous growth in the past years, with over 4.26 billion registered users as of 2021. Image Source: Wikimedia Commons Why does social media make us unhappy? The feeling of insecurity and anxiety after a period of scrolling through meaningless posts...
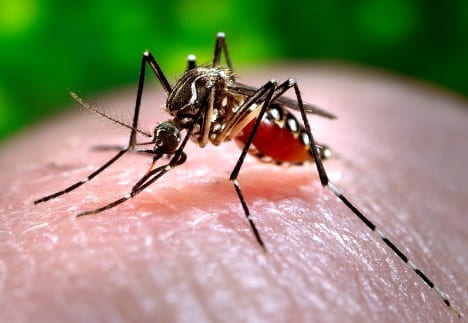
The Viral Secret Behind Mosquito Attraction
Kwabena Boahen Asare ’25, Health Sciences, 22X Figure: Female Aedes Aegypti mosquito sucking human blood. Image Credit: Wikipedia Commons Flaviviruses like Zika and Dengue naturally survive through virus-vector interactions. The vectors of flaviviruses are arthropods, such as mosquitoes, that suck the blood of their vertebrate hosts to nourish their eggs...
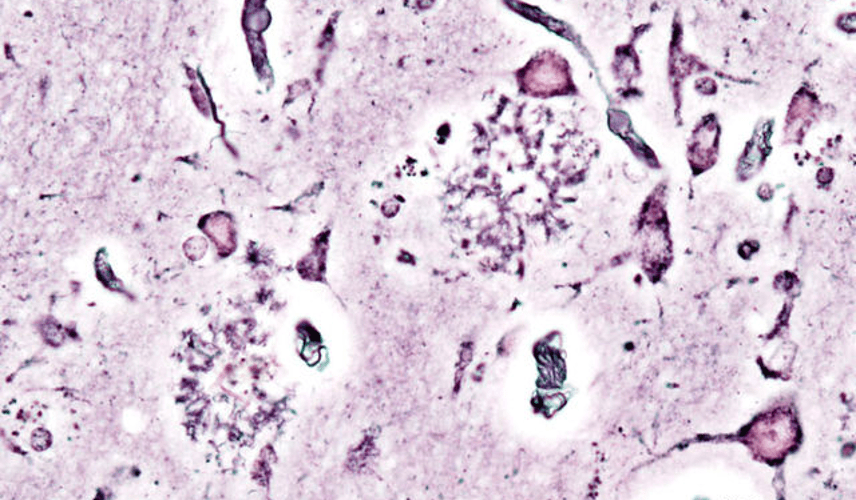
A Cure for Alzheimer’s on the Horizon? Recent Studies show a Cure may be Closer than once Perceived
Luke Putelo ’25, Neuroscience, 22X Figure: Histopathologic picturing of senile plaques seen in the cerebral cortex in a patient with presenile onset of Alzheimer disease Image Source: Wikimedia Commons For years, Alzheimer’s Disease (AD) has stumped researchers; while techniques and procedures have been developed to mitigate the disease, a cure...
A Rigid Brain: The Effects of Anesthesia in Young Children
Evan Accatino ’25, Health Sciences, 22S Figure 1: When children are placed under general anesthesia, they enter a state in which brain activity remains relatively constant. This finding was not observed in anesthetized adults. Image Source: Wikimedia Commons Daily human life is characterized by a continuous cycling between periods of...